Chương trình lớp 8 là một trong những trọng tâm của Toán trung học cơ sở bởi nó có nhiều dạng toán hay và khó. Dưới đây là một dạng bài toán như vậy, xuất hiện nhiều trong các kỳ thi HSG mà học sinh cần nắm vững.
Bài toán 1.
Cho hình vuông ABCD cạnh bằng a. Trên hai cạnh BC, CD lấy lần lượt hai điểm N, M sao cho ∠MAN=450. Trên tia đối của của tia DC lấy điểm I sao cho DI = BN. Hãy tính :
a) Tính số đo ∠IAM
b) Chu vi tam giác CMN theo a.
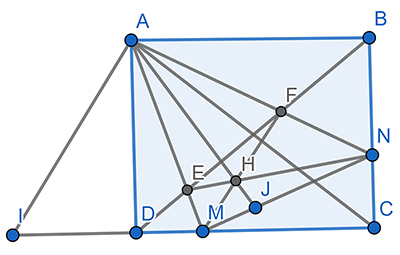
Lời giải:
a. Xét tam giác vuông △ABN và tam giác vuông △ADI có AB = AD, BN = DI ⇒ △ABN = △ADI. Suy ra ∠BAN=∠DAI. (*)
Dễ thấy ∠BAN+∠MAD=450 ⇒ ∠IAM=∠IAD+∠MAD = ∠BAN+∠MAD=450.
a. Xét 2 tam giác △IAM và tam giác △NAM có:
AI = AN (theo (*))
AM chung
Từ kết quả phần b) ta được ∠IAM=∠NAM=450
Suy ra △IAM = △NAM ⇒ MI = MN
Gọi chu vi của tam giác CMN là C ta có: C = CM + MN + NC = CM + MI + NC = CM + MD + BN + NC = BC + CD = 2a.
Bài toán 2.
Cho hình vuông ABCD có độ dài cạnh là a. Một điểm M di động trên cạnh DC(M không trùng D và C). Chọn điểm N trên cạnh BC sao cho ∠MAN=450. Đường chéo DB theo thứ tự cắt AM, AN tại E và F.
a) Chứng minh ΔABF∼ΔACM
b) ∠AFM=∠AEN=900
c) Chứng minh SΔAEF=1/2SΔAMN
d) Chứng minh chu vi tam giác CMN không đổi khi M di động trên DC.
e) Chứng minh rằng khoảng cách từ A đến MN không đổi.
f) Gọi H là giao điểm MF và NE, chứng minh rằng MH.MF + NH.NE = CM2+CN2.
Lời giải:
a. Xét tam giác ΔABF và ΔACM có:
∠ABF=∠ACM=450
∠BAF+∠FAC=450, ∠FAC+∠CAM=450 ⇒ ∠BAF=∠CAM
Suy ra ΔABF∼ΔACM (g.g)
b. Từ kết quả phần a) ΔABF∼ΔACM ⇒ ABAC=AFAM
⇒ ABAF=ACAM
Mặt khác ∠BAC=∠FAM=450
Suy ra ΔABC∼ΔAFM (g.g) ⇒ ∠AFM=900.
Tương tự cũng có ∠AEN=900
c. Dễ dàng chứng minh được ΔAEF∼ΔANM
Sử dụng tính chất: tỉ số giữa diện tích 2 tam giác đồng dạng bằng bình phương tỉ số đồng dạng sẽ được kết quả.
d. Vẽ thêm hình và làm tương tự câu b) của Bài toán 1 nêu trên.
e. Tương tự câu a) của Bài toán 1 nêu trên ta thu được △IAM = △NAM ⇒ AJ = AD = a (không đổi)(2 đường cao xuất phát từ 2 đỉnh tương ứng của 2 tam giác bằng nhau)
f. Bạn đọc có thể dùng tam giác đồng dạng hoặc công thức về cát tuyến với đường tròn để thu được:
MH.MF = MJ.MN
NH.NE = NJ.NM
Suy ra MH.MF + NH.NE = MJ.MN + NJ.NM = MN2 = CM2+CN2.
Bài toán được chứng minh.
MỘT SỐ BÀI TẬP TỰ LUYỆN:
Bài toán 1.
Cho hình vuông ABCD cạnh a. Trên cạnh BC lấy điểm M, trên cạnh CD lấy điểm N sao cho chu vi các tam giác CMN bằng 2a. Đường chéo DB theo thứ tự cắt MN tại E và F.
a) Chứng minh rằng góc
∠MAN có số đo không đổi.
b) Chứng minh ΔABF∼ΔACM
c) ∠AFM=∠AEN=900
d) Chứng minh SΔAEF=1/2SΔAMN
e) Chứng minh rằng khoảng cách từ A đến MN không đổi.
f) Gọi H là giao điểm MF và NE, chứng minh rằng MH.MF + NH.NE = CM2+CN2.
Bài toán 2.
Cho hình vuông ABCD. M là điểm nằm trên cạnh DC. Vẽ tam giác AMN vuông cân tại M (N và A thuộc hai nửa mặt phẳng khác nhau bờ BC). Gọi P là giao điểm của AN và BC.
Chứng minh MA là tia phân giác của góc DMP.
Bài toán 3.
Cho tam giác ABC. Vẽ ra phía ngoài của tam giác các hình vuông BCDE, ACFG, ABKH và các hình bình hành BEQK, CDPF.
Chứng minh tam giác APQ là tam giác vuông cân.
Bài toán 6.
Cho hình vuông ABCD. Gọi E, F lần lượt là trung điểm của AB, BC. Gọi K là giao điểm CE và DF. Chứng minh rằng:
a) CE ⏊ DF
b) Tam giác ADK cân
Bài toán 4.
Cho tứ giác ABCD có ∠B + ∠C = 900, AB = CD. Gọi I, N, J, M lần lượt là trung điểm của AD, AC, CB, DB. Chứng minh rằng INJM là hình vuông.
Bài toán 5.
Cho hình vuông ABCD, I là một điểm nằm trong hình vuông sao cho góc ∠IBC = ∠ICB = 150, J là một điểm nằm ngoài hình vuông sao cho góc ∠JDC = ∠JCD = 600. Chứng minh rằng:
a) Tam giác AID là tam giác đều.
b) Ba điểm B, I, J thẳng hàng.
Nguyễn Kim Sổ
Hội Toán học Hà Nội