Bài toán 1. (Đề minh họa của SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI cho kỳ thi tuyển sinh vào lớp 10 THPT, theo Chương trình GDPT 2018, kèm thông báo số 2998/TB–SGDĐT ngày 28/08/2024)
Trong buổi tham quan dã ngoại cuối năm, mỗi khối lớp 9 được dùng một tấm bạt hình chữ nhật ABCD cùng loại, có chiều dài 10m, chiều rộng 6m; với M, N là trung điểm các cạnh AD, BC (hình 1).
Mỗi lớp sử dụng tấm bạt như trên để dựng thành chiếc lều có dạng hình lăng trụ đứng tam giác (hình 2); hai đáy hình lăng trụ là hai tam giác cân: tam giác ADM và tam giác BNC, với độ dài cạnh đáy của hai tam giác cân là x(m). (Tấm bạt chỉ dùng để dựng thành mái lều, không trải thành đáy lều). Tìm x để thể tích không gian trong lều là lớn nhất.
Bản PDF hướng dẫn giải chi tiết các em học sinh có thể tải về TẠI ĐÂY
Bài toán 2. (Đề tham khảo của SỞ GIÁO DỤC VÀ ĐÀO TẠO TP. HỒ CHÍ MINH cho kỳ thi tuyển sinh vào lớp 10 THPT, theo Chương trình GDPT 2018)
Một quả dưa hấu không hạt, ruột đỏ có dạng hình cầu đường kính 25cm và phần vỏ dày 2cm.
a) Coi phần ruột màu đỏ cũng có dạng hình cầu và có cùng tâm với quả dưa hấu. Tính thể tích phần ruột quả dưa hấu. (Kết quả làm tròn đến hàng trăm của $cm^3$).
b) Người ta ép phần ruột màu đỏ của quả dưa hấu trên thì thể tích nước ép thu được bằng 80% thể tích phần ruột. Nước ép sẽ được đựng trong các ly thủy tinh giống nhau, phần lòng trong dạng hình trụ có chiều cao 10cm và đường kính đáy là 5cm. Mỗi ly chỉ chứa 70% thể tích. Hỏi để đựng nước ép của quả dưa hấu nói trên thì cần ít nhất bao nhiêu cái ly?
Biết công thức tính thể tích hình trụ là V = $πR^2h$ (R là bán kính đáy, h là chiều cao); công thức tính thể tích hình cầu là V = $\frac{4}{3}πR^3$ (R là bán kính hình cầu).
Phân tích hướng giải và bình luận:
a) Ta tính được bán kính (hình cầu) phần ruột màu đỏ của quả dưa hấu là: R = (25 - 2.2)/2 = 10,5 (cm).
Sử dụng công thức V = $\frac{4}{3}πR^3$ ta tính được thể tích phần ruột quả dưa hấu là: $V_{1}$ = $4/3.π.10,5^3$ ≈ 4849,05 ($cm^3$).
b) Thể tích nước ép $V_{E}$ thu được khi ép phần ruột màu đỏ của quả dưa hấu là: $V_{E}$ = 80%$V_{1}$ ≈ 3879,24 ($cm^3$ ).
Thể tích mỗi chiếc ly là: $V_{2}$ = $πR^2h$ = $π.\left(\frac{5}{2}\right)^{2}.10$ ≈ 196,35 ($cm^3$).
Thể tích chứa nước quy định của mỗi ly là: $V_{N}$ = 70%V_2 ≈ 137,44 ($cm^3$).
Khi đó $\frac{V_{E}}{V_{N}}$ ≈ $\frac{3879,24}{137,44}$ = 28,22.
Do đó cần ít nhất 29 chiếc ly để đựng hết nước ép từ quả dưa hấu nói trên.
Bài toán 3. (Nguyễn Bá Đang – Seminar của Hội toán học Hà Nội, ngày 03/10/2024)
Một học sinh gấp tờ giấy hình chữ nhật với độ dài các cạnh là a; b (a > b > 0) sao cho hai đỉnh đối diện trùng nhau tạo thành một ngũ giác. Tính tỉ số giữa diện tích hình ngũ giác và hình chữ nhật ban đầu.
Phân tích hướng giải và bình luận:
Như hình vẽ trên, khi gập hình chữ nhật ABCD sao cho C trùng với A để tạo thành ngũ giác ADNPQ thì NA = NC, PA = PC do đó NP sẽ là đường trung trực của AC và ANCP sẽ là một hình thoi.
Khi đó diện tích ngũ giác ADNPQ gấp hai lần diện tích tứ giác AMPQ.
Sử dụng định lý Pythagoras ta có: $AC^2$ = $AB^2$ + $BC^2$ = $a^2$ + $b^2$
AC = $\sqrt{a^{2}+b^{2}}$
Hai tam giác vuông AMP và ABC đồng dạng nên:
$\frac{AM}{AB}=\frac{AP}{AC}=\frac{MP}{BC}$ suy ra:
AP =$\frac{AM}{AB}.AC$ = $\frac{\frac{\sqrt{a^{2}+b^{2}}}{2}}{a}.\sqrt{a^{2}+b^{2}}$ = $\frac{a^{2}+b^{2}}{2a}$
MP =$\frac{AM}{AB}.BC$ = $\frac{\frac{\sqrt{a^{2}+b^{2}}}{2}}{a}.b$ = $\frac{b\sqrt{a^{2}+b^{2}}}{2a}$
BP = AB – AP = a – $\frac{a^{2}+b^{2}}{2a}$ = $\frac{a^{2}-b^{2}}{2a}$
Khi đó diện tích tứ giác AMPQ xác định bởi:
$S_{AMPQ}$= $S_{AMP}+S_{APQ}= S_{AMP}+S_{BCP}$
= $\frac{1}{2}MA.MP+ \frac{1}{2}BC.BP$
= $\frac{1}{2}\frac{\sqrt{a^{2}+b^{2}}}{2}.\frac{b\sqrt{a^{2}+b^{2}}}{2a}+ \frac{1}{2}b.\frac{a^{2}-b^{2}}{2a}$
= $\frac{b(3a^{2}-b^{2})}{8a}$
$S_{ADNPQ}$ = $2S_{AMPQ}$ = $\frac{b(3a^{2}- b^{2})}{4a}$
Từ đây ta tính được: k = $\frac{S_{ADNPQ }}{S_{ABCD }}$ = $\frac{\frac{b(3a^{2}- b^{2})}{4a}}{ab}$ = $\frac{3a^{2}- b^{2}}{4a^{2}}$.
Bài toán 4. Một tấm bìa hình vuông có cạnh 24cm. Ở mỗi góc người ta cắt đi một hình vuông nhỏ kích thước như nhau rồi gấp lên để tạo thành chiếc hộp có dạng hình hộp chữ nhật không nắp.
Tìm độ dài cạnh hình vuông nhỏ phải cắt để chiếc hộp thu được có thể tích lớn nhất.
Phân tích hướng giải và bình luận:
Điều kiện: 2x < 24 hay x < 12.
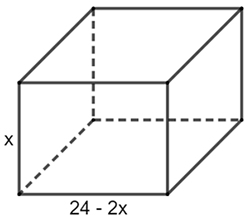
Khi đó độ dài cạnh hình vuông đáy hộp là 24 – 2x và thể tích chiếc hộp được xác định bởi công thức:
V = $x(24-2x)^{2}$ = $4x(12-x)^{2}$ = 2[2x(12 – x)(12 – x)].
Sử dụng bất đẳng thức Cauchy với ba số ta có:
V = 2[2x(12 – x)(12 – x)] ≤ $2\left(\frac{2x + 12 - x + 12 - x}{3}\right)^{3}$ = 1024.
Dấu “=” xảy ra khi 2x = 12 – x hay x = 4 (thỏa mãn điều kiện).
Vậy ta phải cắt mỗi góc một hình vuông nhỏ có cạnh là 4cm để chiếc hộp thu được có thể tích lớn nhất.
Bài toán 5. (Đề thi kiểm tra kiến thức định kỳ môn Toán lớp 9, Trung tâm Bồi dưỡng và Phát triển tài năng Toán học Nam Sáng – tháng 9, năm 2024)
Gia đình bác Đức dự định xây một bể âm nhỏ (loại bể nằm sâu dưới lòng đất) trước sân nhà để muôi cá cảnh. Bể có dạng hình hộp chữ nhật có đáy là hình vuông và thể tích nước chứa tối đa 4$m^3$. Sau khi đào xong bác sẽ tiến hành xây xung quanh (bao gồm cả đáy), thành của bể được xây cao hơn mặt đất 20cm. Hãy xác định kích thước của bể cũng như chiều sâu phải đào để khi xây tiết kiệm nguyên vật liệu nhất.
Phân tích hướng giải và bình luận:
Ta gọi x (m) là độ dài cạnh hình vuông đáy bể, gọi y (m) là chiều cao của thành bể sau khi xây.
Điều kiện: x, y > 0.
Khi đó ta có phương trình theo thể tích: $x^2$y = 4.
Diện tích cần xây S sẽ bao gồm diện tích xung quanh và đáy bể được xác định bởi: S = 4xy + $x^2$ (*).
Từ $x^2y$ = 4 rút ra: y = 4/x^2 thay vào (*) ta được: S = $\frac{16}{x}+x^2$.
Thử một vài giá trị x nguyên là ước của 16 và dự đoán điểm rơi tại x = 2, ta xét hiệu:
S – 12 = $\frac{16}{x}+x^2$ – 12 = $ \frac{(x-2)^{2}(x+4)}{x}$∙
Vì $(x-2)^{2}$ ≥ 0 và (x + 4) > 0 nên $ \frac{(x-2)^{2}(x+4)}{x}$ ≥ 0 hay S ≥ 12.
Dấu “=” xảy ra khi x = 2 và y = 1. Khi đó độ sâu phải đào là 100 – 20 = 80 (cm).
Vậy để khi xây tiết kiệm nguyên vật liệu nhất thì bể phải có kích thước: cạnh đáy 2 m, chiều cao 1 m và độ sâu cần đào là 80 cm.
Ngoài ra các em cũng có thể dùng bất đẳng thức Cauchy với ba số để tìm GTNN của S như sau:
S = $\frac{16}{x}+x^2$ = $\frac{6}{x}+\frac{8}{x}+x^2$ ≥ 3$\sqrt[3]{\frac{6}{x}.\frac{8}{x}.x^2}$ = 12.
Dấu “=” xảy ra khi x = 2 và y = 1.
Các em cũng thu được kết quả tương tự.
Bài toán 6. Trong giờ thực hành về hình học trực quan, học sinh gấp một miếng bìa hình chữ nhật có chiều dài 60cm; chiều rộng 30cm theo các đường thẳng BB’, CC’ và DD’ (hình 1) sao cho EG trùng với AA’ để được chiếc hộp đứng có dạng hình hộp chữ nhật (hình 2).
Hai đáy trên và dưới sẽ được cắt từ miếng bìa khác để ghép vào. Hãy xác định x và y để thể tích chiếc hộp thu được là lớn nhất.
Phân tích hướng giải và bình luận:
Ta biểu diễn được $V_{ABCD.A’B’C’D’}$ = AA’.$S_{ABCD}$ = 30xy (1).
Theo bài ra thì: 2x + 2y = 60, suy ra y = 30 – x. Thay vào (1) ta được:
$V_{ABCD.A’B’C’D’}$ = 30x(30 – x).
Từ $(a – b)^2$ ≥ 0 ∀ a, b ∈ R suy ra 4ab ≤ $(a + b)^2$ hay ab ≤ $(\frac{a + b}{2})^{2}$∙
Dấu “=” xảy ra khi a = b. Áp dụng vào bài toán ta có:
$V_{ABCD.A’B’C’D’}$ = 30[x(30 - x)] ≤ $30(\frac{x + 30 - x}{2})^{2}$ = 6750.
Dấu “=” xảy ra khi: x = 30 – x suy ra: x = 15 và y = 30 – 15 = 15 (thỏa mãn điều kiện).
Vậy khi x = y = 15 cm thì thể tích chiếc hộp đạt giá trị lớn nhất và giá trị đó là 6750 $cm^2$.
Thực ra đây chính là kết quả quen thuộc: Trong tất cả các hình chữ nhật có cùng chu vi thì hình vuông là hình có diện tích lớn nhất.
MỘT SỐ BÀI TOÁN TỰ LUYỆN.
Bài toán 7. (Đề kiểm tra giữa học kì 1 – môn Toán lớp 9, Trường THCS & THPT M.V.LÔ-MÔ-NÔ-XỐP, năm học 2024 – 2025)
Bác Sơn muốn xây một bể chứa nước dạng hình hộp chữ nhật không nắp, có thể tích bằng 36$m^3$. Đáy bể là hình chữ nhật có chiều rộng là x (m) và chiều dài gấp đôi chiều rộng. Bác Sơn muốn phần diện tích cần xây (bao gồm diện tích xung quanh và đáy bể) là nhỏ nhất để tiết kiệm chi phí thì x phải bằng bao nhiêu?
Bài toán 8. Một miếng bìa hình vuông ABCD có cạnh là 30 cm . Trên cạnh AB lấy hai điểm M , P sao cho AM = PB = x (cm) và điểm M nằm giữa điểm A và điểm P. Qua M kẻ đường thẳng vuông góc với AB cắt CD tại N ; qua P kẻ đường thẳng vuông góc với AB cắt CD tại Q (hình 1).
Người ta gập miếng bìa theo hai cạnh MN và PQ sao cho cạnh BC trùng cạnh AD như hình vẽ để tạo thành hình lăng trụ đứng AMPDNQ (hình 2). Hai đáy trên và dưới sẽ được cắt từ miếng bìa khác để ghép vào. Hãy xác định x để thể tích hình lăng trụ là lớn nhất.
NGUYỄN KIM SỔ
Hội Toán học Hà Nội