Bài toán P, NP và đặc biệt là mối quan hệ giữa P và NP là một bài toán mở quan trọng trong lý thuyết khoa học máy tính và cũng không sai khi nói rằng nó quan trọng bậc nhất của thời đại hiện nay - kỷ nguyên số 4.0.
Đây là một trong bảy bài toán nổi tiếng và phức tạp, được lựa chọn bởi Viện Toán học Clay vào ngày 24 tháng 5 năm 2000. Viện này cũng đồng thời treo phần thưởng trị giá một triệu đô cho bất cứ ai có được lời giải chính xác cho mỗi bài toán trong danh sách này. Tính tới nay, chỉ có duy nhất một bài toán trong danh sách này mới được giải, đó là giả thuyết Poincaré bởi nhà toán học người Nga Grigori Yakovlevich Perelman vào năm 2010.
Bài toán P:
Là bài toán người ta có thể chỉ ra thuật toán để giải nó(tạm gọi là tìm nghiệm) trong thời gian đa thức.
Chúng ta sẽ cùng tìm hiểu qua một vài ví dụ đơn giản:
Ví dụ 1: Cho một dãy số gồm n số hạng, hãy tìm phần tử lớn nhất.
Một cách đơn giản là duyệt từ đầu đến cuối, mỗi lần duyệt là một phép so sánh và cuối cùng qua n bước ta thu được kết quả. Người ta nói rằng độ phức tạp của thuật toán này là đa thức O(n). Tất nhiên trong thực tế thì mỗi phép tính như cộng trừ nhân chia, khai căn đều có độ phức tạp riêng của nó nhưng cái này là bản thân máy làm, chúng ta không can thiệp nên thời không tính vào đây(việc cải tiến phụ thuộc vào người viết hệ điều hành và phát triển phần cứng)
Nếu giải thuật nào cần đến a.$n^2$ + bn + c phép tính để cho ra kết quả thì khi n lớn (bn + c) là không đáng kể so với $n^2$ nên người ta lấy bậc cao nhất(tăng nhanh nhất), loại bỏ hằng số và coi bài toán này có độ phức tạp O($n^2$)…Nói chung khi nó vẫn là các đa thức dù là bậc bao nhiêu đi nữa cũng gộp chung lại thành lớp các bài toán P.
Ví dụ 2: Cho tập hợp gồm n phần tử, tìm tập con có tổng bằng 0(nếu có).
Bình thường ta có thể thấy tập này có $2^n$ - 1 tập con(bỏ tập rỗng), nếu ta dùng $2^n$ – 1 phép duyệt, mỗi lần đi tới 1 tập con ta tính tổng rồi so sánh với 0. Độ phức tạp của tính tổng O(n) cũng tham gia vào đây nhưng vì khi n lớn n quá bé so với $2^n$ nên người ta cũng bỏ qua và coi bài toán này có độ phức tạp O($2^n$) tức là độ phức tạp hàm mũ.
Ngoài ra còn có những thuật toán với độ phức tạp khác như: n!, O(nlogn), O(logn)…
Bởi vì hàm đa thức tăng chậm hơn hàm mũ và hàm lũy thừa nên lớp các bài toán P được coi là “dễ” theo quan điểm của toán-tin lý thuyết. Hoặc nhìn hàm n! có vẻ đẹp nhưng thực tế là rất tệ, đã có một bài toán trong đề thi vô địch Poland 1982: So sánh 2 số $(17091982!)^2$ và $17091982^{17091982}$ mà khi chứng minh nó học sinh còn tổng quát được $(n!)^2$ > $n^n$ nghĩa là khối lượng tính toán còn tăng khủng khiếp hơn độ phức tạp lũy thừa rất nhiều khi kích thước(n) của bài toán lớn.
Người ta đã đưa ra biểu đồ so sánh và nhận định thế này:
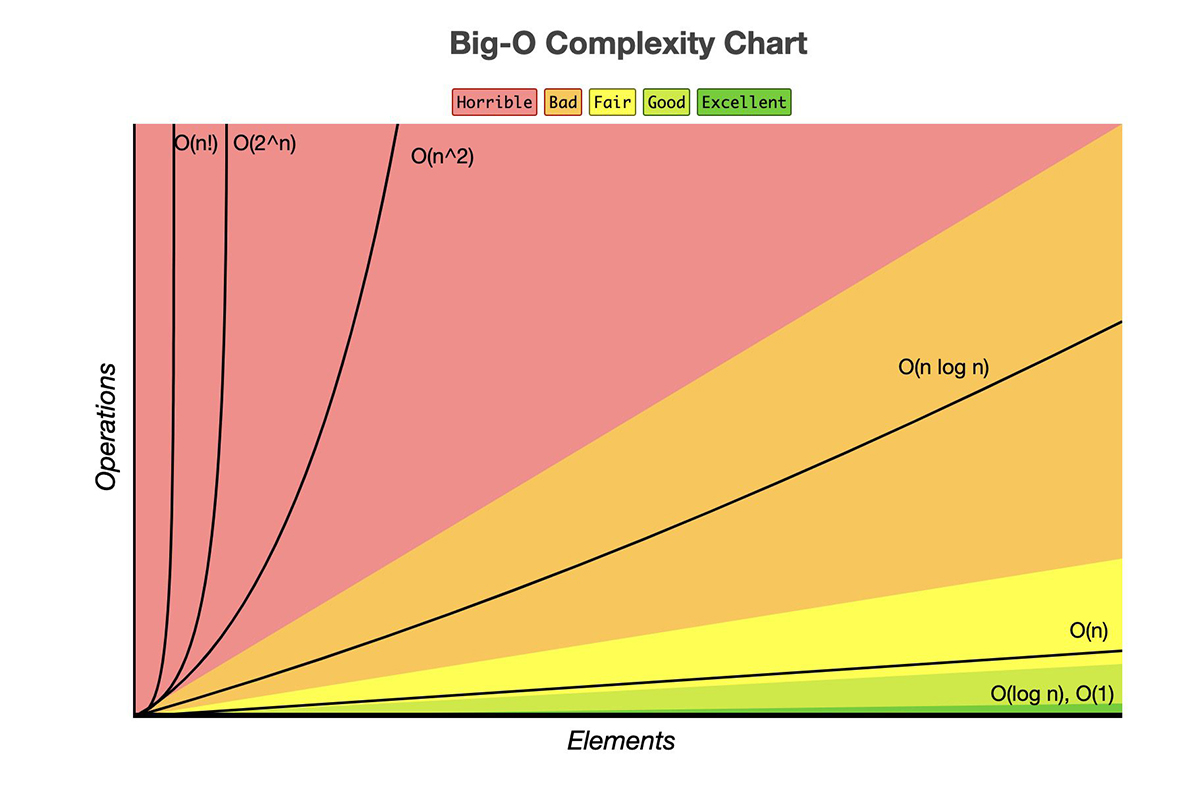
Bài toán NP:
Là bài toán chưa tìm được giải thuật với độ phức tạp đa thức nhưng chỉ ra được phương pháp kiểm định nghiệm của nó(nếu có) với thời gian đa thức.
Để rõ hơn chúng ta lại quay về ví dụ 2 nêu trên. Giả sử tập A = {-1, 2, 3, -4, -5, 6} lúc này n = 6 và có thể thấy tập B = {-1, 2, 3, -4} là một tập con thỏa mãn yêu cầu bài ra và việc kiểm chứng nó dựa vào phép duyệt qua tất cả 4 phần tử với 4 phép tính cộng, rõ ràng thỏa mãn 2 điều kiện:
+ phép kiểm chứng này độ phức tạp đa thức
+ thuật toán tìm các tập con như thế với độ phức tạp đa thức là chưa có)
nên được xếp vào lớp NP!
Có thể thấy rằng một bài toán dễ giải thì cũng dễ kiểm tra lời giải nên ta có mối quan hệ P ⊆ NP.
Khi nghiên cứu các bài toán lớp NP người ta quan tâm đến NP-complete(NP đầy đủ) là tập những bài toán thuộc dạng khó nhất. Hai nhà toán học Cook và Levin chứng minh được rằng mọi bài toán thuộc lớp NP đều đưa được về một bài toán NP-complete cho trước bằng một phép biến đổi sử dụng một lượng thời gian là đa thức. Như vậy, chỉ cần một bài toán NP-complete có lời giải với thời gian đa thức, là đủ để khẳng định P = NP.
Đây là vấn đề thú vị, cũng giống như để chứng minh định lý Fermat lớn nhà toán học Andrew Wiles với 7 năm ròng rã chỉ đi chứng minh giả thuyết Taniyama-Shimura về mối quan hệ giữa đường cong elip và các dạng modular của lý thuyết số(đưa ra khoảng 1955) thì biết đâu trong số các nhà toán học của Việt Nam mình sẽ có người tìm ra thuật toán giải bài toán NP-complete khi đó cũng là điểm kết thúc cho bài toán thiên niên kỷ hóc búa này.
Quay trở lại với thực tế, toán - tin lý thuyết đã đi trước chúng ta hàng thế kỷ. Những bài toán lớp P được cho là “dễ giải” đó nhưng với công nghệ hiện tại vẫn không dễ chút nào. Ví dụ một siêu máy tính ở Việt nam là hệ thống tính toán hiệu năng cao của Viettel đạt 20 PetaFlops (20 triệu tỷ phép tính/giây), một ngày được khoảng 1021 phép tính. Như thế nếu chạy 1 thuật toán của bài toán lớp P có độ phức tạp O(n) với n là số có 25 chữ số sẽ mất khoảng $10^{24}$/$10^{23}$ ~ 3 năm!
Để tìm được số nguyên tố lớn nhất(dạng Mersenne) như hiện nay với hơn 9 triệu chữ số thì nhà khoa học thuộc Đại học Missouri - Mỹ, đã sử dụng hơn 700 máy tính tương đương với khả năng xử lý của của một máy tính Pentium 90MHz chạy liên tục trong 67.000 năm!
Những ví dụ đó đủ cho thấy rằng nhân loại tuy có nhiều tiến bộ nhưng những gì thu được còn rất nhỏ bé so với vũ trụ bao la, ngoài kia biết đâu có người ngoài hành tinh và nền khoa học công nghệ của họ đã đạt đến mức siêu nhiên như các nhà khoa học viễn tưởng nhận định [1]. Việc giải quyết mối quan hệ giữa P - NP và cải tiến hiệu năng của các siêu máy tính sẽ tác động trực tiếp tới vấn mã hóa và bảo mật thông tin hiện nay.
Đến một câu hỏi đặt ra là khi khoa học máy tính phát triển đến mức siêu nhiên như thế mà ai đó giải được bài toán mối quan hệ thật sự giữa P và NP đặc biệt đưa ra kết luận P = NP thì vấn đề bảo mật thông tin tính thế nào khi các thuật toán mã hóa không còn giá trị - bởi vì các hệ mã hoá hiện nay đều được xây dựng dựa trên niềm tin rằng P ≠ NP. Một ví dụ kinh điển là thuật toán mật mã hóa khóa công khai RSA(được dùng trong các giao dịch điện tử, tạo chữ ký số cho văn bản…) dựa trên bài toán NP: phân tích một số nguyên lớn thành tích các thừa số nguyên tố.
Ngay cả với chúng ta hiện tại, mọi thứ đều được lưu trữ ở dạng dữ liệu nên vấn đề bảo mật thông tin là vấn đề sống còn với mỗi cá nhân, doanh nghiệp, quốc gia. Nếu N = NP những thứ được tin là an toàn, sẽ không còn an toàn nữa. Bitcoin, Etherium, blockchain cũng sẽ gặp vấn đề. User-password của mỗi người trên điện thoại, máy tính, mạng xã hội, tài khoản ngân hàng cũng trở thành nỗi đắn đo. Nhưng cũng như đã trình bày thêm ở mục [1]: nhân loại tuy có nhiều tiến bộ nhưng những gì thu được còn rất nhỏ bé, năng lực các cỗ máy còn hạn chế và nếu N = NP có xảy ra đi nữa thì người ta cũng sẽ đi tìm những thuật toán mới và trong thời gian chờ đợi ta tăng chiều dài khóa bảo mật lên, bởi thuật toán để giải các bài toán NP-complete dù là đa thức thì cũng mất rất nhiều thời gian nên trong tương lai gần chúng ta cũng vẫn được bảo vệ…
Hà Nội, ngày 17 tháng 03 năm 2023
Nguyễn Kim Sổ
Hội Toán học Việt Nam